Can a 3 Axis Arm Draw a Circle
Annotation: These are working notes used for a course beingness taught at MIT. They will exist updated throughout the Fall 2021 semester.
Basic Pick and Place
The stage is set. Yous have your robot. I take a little ruby foam brick. I'm going to put information technology on the table in front of your robot, and your goal is to move information technology to a desired position/orientation on the table. I want to defer the perception trouble for one affiliate, and volition permit yous assume that you have access to a perfect measurement of the current position/orientation of the brick. Even without perception, completing this task requires us to build up a basic toolkit for geometry and kinematics; it's a natural identify to start.
First, nosotros volition establish some terminology and annotation for kinematics. This is 1 area where careful note tin can yield dividends, and sloppy notation will inevitably lead to defoliation and bugs. The Drake developers take gone to great length to establish and certificate a consequent multibody notation, which we call "Monogram Notation". The documentation even includes some of the motivation/philosophy backside that note. I'll use the monogram notation throughout this text.
If you'd like a more extensive background on kinematics than what I provide hither, my favorite reference is all the same
Please don't get overwhelmed by how much background material in that location is to know! I am personally of the opinion that a clear agreement of just a few bones ideas should brand you very effective hither. The details will come up later, if you need them.
Monogram Notation
The following concepts are disarmingly subtle. I've seen incredibly smart people presume they knew them and and so perpetually stumble over notation. I did it for years myself. Have a minute to read this carefully!
Maybe the most cardinal concept in geometry is the concept of a betoken. Points occupy a position in infinite, and they tin can have names, e.g. point $A$, $C$, or more descriptive names like $B_{cm}$ for the heart of mass of body $B$. We'll denote the position of the point by using a position vector $p^A$; that'southward $p$ for position, and not for point, because other geometric quantities tin can too accept a position.
Merely allow'south be more careful. Position is actually a relative quantity. Really, we should merely ever write the position of 2 points relative to each other. We'll employ due east.1000. $^Ap^C$ to announce the position of $C$ relative to $A$. The left superscript looks mighty strange, but we'll see that it pays off in one case we start transforming points.
Every time nosotros describe the (relative) position as a vector of numbers, we need to be explicit about the frame we are using, specifically the "expressed-in" frame. All of our frames are defined by orthogonal unit of measurement vectors that follow the "right-hand rule". We'll give a frame a name, also, like $F$. If I want to write the position of point $C$ relative to point $A$, expressed in frame $F$, I will write $^Ap^C_F$. If I ever want to become simply a single component of that vector, eastward.1000. the $ten$ component, then I'll use $^Ap^C_{F_x}$.
That is seriously heavy notation. I don't love it myself, just it's the nearly durable I've got, and we'll take shorthand for when the context is articulate.
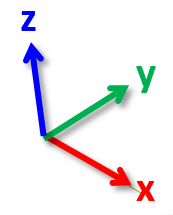There are a few very special frames. We use $Westward$ to denote the world frame. We think about the world frame in Drake using vehicle coordinates (positive $x$ to the front, positive $y$ to the left, and positive $z$ is up). The other particularly special frames are the body frames: every torso in the multibody system has a unique frame attached to information technology. We'll typically utilise $B_i$ to denote the frame for body $i$.
Frames have a position, too -- it coincides with the frame origin. So it is perfectly valid to write $^Wp^A_W$ to announce the position of signal $A$ relative to the origin of the world frame, expressed in the world frame. Here is where the shorthand comes in. If the position of a quantity is relative to a frame, and expressed in the aforementioned frame, then we can safely omit the subscript. $^Fp^A \equiv {^Fp^A_F}$. Furthermore, if the "relative to" field is omitted, then we presume that the point is relative to $W$, so $p^A \equiv {}^Wp^A_W$.
Frames also have an orientation. We'll use $R$ to denote a rotation, and follow the aforementioned note, writing $^BR^A$ to denote the rotation of frame $A$ relative to frame $B$. Unlike vectors, pure rotations exercise not take an additional "expressed in" frame.
A frame $F$ can be specified completely by a position and rotation relative to another frame. Taken together, we call the position and rotation a spatial pose, or just pose. A spatial transform, or simply transform, is the "verb form" of pose. In Drake we use RigidTransform to correspond a pose/transform, and denote it with the alphabetic character $X$. $^BX^A$ is the pose of frame $A$ relative to frame $B$. When we talk near the pose of an object $O$, without mentioning a reference frame explicitly, we mean $^WX^O$ where $O$ is the body frame of the object. Nosotros exercise not utilize the "expressed in" frame subscript for pose; we always desire the pose expressed in the reference frame.
The Drake documentation also discusses how to use this notation in code. In short, $^Bp^A_C$ is written p_BA_C, ${}^BR^A$ as R_BA, and ${}^BX^A$ equally X_BA. It works, I hope.
Selection and place via spatial transforms
At present that we have the notation, we tin formulate our approach to the bones pick and place trouble. Permit us call our object, $O$, and our gripper, $G$. Our arcadian perception sensor tells usa $^WX^O$. Let's create a frame $O_d$ to describe the "desired" pose of the object, $^WX^{O_d}$. So choice and identify manipulation is simply trying to make $X^O = X^{O_d}$.
To reach this, we volition presume that the object doesn't move relative to the world ($^WX^O$ is abiding) when the gripper is open up, and the object doesn't move relative to the gripper ($^GX^O$ is constant) when the gripper is airtight. Then we can:
- motion the gripper in the world, $X^1000$, to an appropriate pose relative to the object: $^OX^{G_{grasp}}$.
- shut the gripper.
- move the gripper+object to the desired pose, $X^O = Ten^{O_d}$.
- open the gripper, and retract the manus.
To simplify the trouble of approaching the object (without colliding with it) and retracting from the object, we will insert a "pregrasp pose", $^OX^{G_{pregrasp}}$, above the object as an intermediate step.
Conspicuously, programming this strategy requires good tools for working with these transforms, and for relating the pose of the gripper to the joint angles of the robot.
Spatial Algebra
Hither is where we start to see the pay-off from our heavy notation, as we define the rules of converting positions, rotations, poses, etc. between different frames. Without the notation, this invariably involves me with my right hand in the air making the "right-mitt rule", and my head twisting around in space. With the notation, it'south a simple thing of lining up the symbols properly, and nosotros're more than likely to get the right answer!
Here are the bones rules of algebra for our spatial quantities:
- Positions expressed in the aforementioned frame can be added when their reference and target symbols match: \begin{equation}{}^Ap^B_F + {}^Bp^C_F = {}^Ap^C_F.\stop{equation} The condiment inverse is well defined: \begin{equation}{}^Ap^B_F = - {}^Bp^A_F.\cease{equation} Those should be pretty intuitive; make sure you confirm them for yourself.
- Multiplication past a rotation tin be used to change the "expressed in" frame: \brainstorm{equation}{}^Ap^B_G = {}^GR^F {}^Ap^B_F.\terminate{equation} Y'all might exist surprised that a rotation alone is enough to alter the expressed-in frame, only it'southward true. The position of the expressed-in frame does non affect the relative position betwixt 2 points.
- Rotations tin can be multiplied when their reference and target symbols match: \begin{equation}{}^AR^B \: {}^BR^C = {}^AR^C.\end{equation} The inverse performance is too simply defined: \brainstorm{equation}\left[{}^AR^B\right]^{-1} = {}^BR^A.\end{equation} When the rotation is represented as a rotation matrix, this is literally the matrix changed, and since rotation matrices are orthonormal, we also take $R^{-1}=R^T.$
- Transforms bundle this up into a single, convenient annotation when positions are relative to a frame (and the same frame they are expressed in): \begin{equation}{}^Gp^A = {}^GX^F {}^Fp^A = {}^Gp^F + {}^Fp^A_G = {}^Gp^F + {}^GR^F {}^Fp^A.\end{equation}
- Transforms compose: \begin{equation}{}^AX^B {}^BX^C = {}^AX^C,\end{equation} and have an inverse \brainstorm{equation}\left[{}^AX^B\right]^{-1} = {}^BX^A.\end{equation} Please note that for transforms, we generally exercise non take that $X^{-one}$ is $X^T,$ though it still has a simple form.
In practice, transforms are implemented using homogenous coordinates, but for now I'm happy to get out that as an implementation detail.
From photographic camera frame to world frame
Imagine that I have a depth camera mounted in a stock-still pose in my workspace. Let's telephone call the camera frame $C$ and announce its pose in the world with ${}^WX^C$. This pose is often called the camera "extrinsics".
A depth camera returns points in the camera frame. Therefore, nosotros'll write this position of point $P_i$ with ${}^Cp^{P_i}$. If nosotros want to convert the point into the earth frame, we simply have $$p^{P_i} = Ten^C {}^Cp^{P_i}.$$
This is a work-horse operation for us. We often aim to merge points from multiple cameras (typically in the globe frame), and always demand to somehow relate the frames of the camera with the frames of the robot.
Forward kinematics
The spatial algebra gets us pretty shut to what we need for our option and place algorithm. But think that the interface we have with the robot reports measured articulation positions, and expects commands in the class of joint positions. So our remaining task is to convert between joint angles and cartesian frames. We'll exercise this in steps, the starting time step is to become from joint positions to cartesian frames: this is known as forward kinematics.
Throughout this text, we will refer to the articulation positions of the robot (besides known as "configuration" of the robot) using a vector $q$. If the configuration of the scene includes objects in the environment as well as the robot, we would use $q$ for the entire configuration vector, and use e.grand. $q_{robot}$ for the subset of the vector respective to the robot'southward articulation positions. Therefore, the goal of forrad kinematics is to produce a map: \brainstorm{equation}Ten^Chiliad = f_{kin}^Grand(q).\end{equation} Moreover, we'd like to have forward kinematics available for whatsoever frame we have defined in the scene. Our spatial notation and spatial algebra makes this ciphering relatively direct-forward.
The kinematic tree
In order to facilitate kinematics and related multibody computations, the MultibodyPlant organizes all of the bodies in the world into a tree topology. Every body (except the world trunk) has a parent, which it is continued to via either a Joint or a "floating base of operations".
Inspecting the kinematic tree
Drake provides some visualization support for inspecting the kinematic tree information structure. The kinematic tree for an iiwa is more of a vine than a tree (it'south a serial manipulator), just the tree for the dexterous hands are more interesting. I've added our brick to the case, too, so that you tin can see that a "costless" torso is just another branch off the world root node.
Every Joint and "floating base" has some number of position variables associated with information technology -- a subset of the configuration vector $q$ -- and knows how to compute the configuration dependent transform beyond the joint from the child joint frame $J_C$ to the parent joint frame $J_P$: ${}^{J_P}X^{J_C}(q)$. Additionally, the kinematic tree defines the (fixed) transforms from the joint frame to the child body frame, ${}^CX^{J_C}$, and from the joint frame to the parent frame, ${}^PX^{J_P}$. Altogether, we can compute the configuration transform between any one torso and its parent, $${}^PX^C(q) = {}^PX^{J_P} {}^{J_P}X^{J_C}(q) {}^{J_C}X^C.$$
Specifying the kinematic tree in URDF
Specifying the kinematic tree in SDF
You might be tempted to think that every time you add a articulation to the MultibodyPlant, you are calculation a degree of freedom. Only information technology actually works the other way around. Every time yous add together a trunk to the plant, you are calculation many degrees of liberty. But you can and then add joints to remove those degrees of freedom; joints are constraints. "Welding" the robot's base to the globe frame removes all of the floating degrees of freedom of the base of operations. Adding a rotational articulation between a kid body and a parent body removes all just one degree of freedom, etc.
Forward kinematics for pick and place
In order to compute the pose of the gripper in the world, $X^G$, we but query the parent of the gripper frame in the kinematic tree, and recursively compose the transforms until nosotros get to the globe frame.
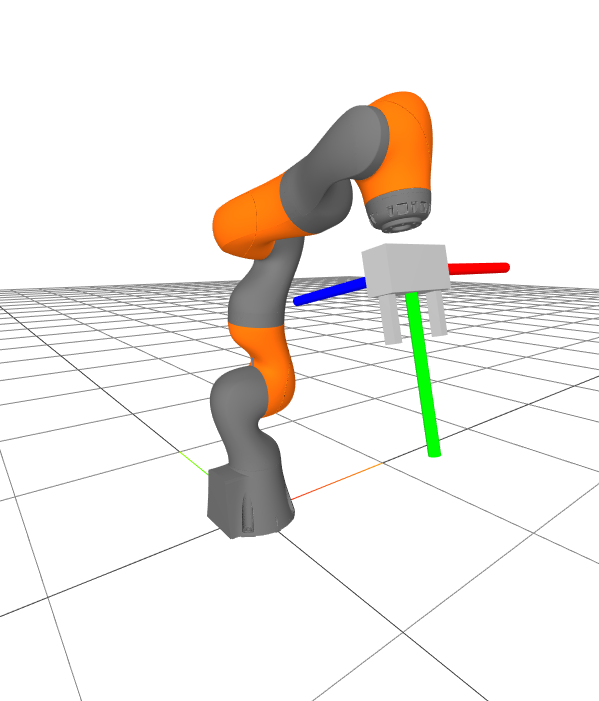
Forward kinematics for the gripper frame
Let'southward evaluate the pose of the gripper in the world frame: $X^M$. We know that information technology will exist a role of configuration of the robot, which is just a function of the full state of the MultibodyPlant. The following case shows you how it works.
The key lines are
gripper = plant.GetBodyByName("trunk") pose = plant.EvalBodyPoseInWorld(context, gripper) Backside the scenes, the MultibodyPlant is doing all of the spatial algebra we described higher up to render the pose (and besides some clever caching because y'all tin can reuse much of the computation when you want to evaluate the pose of another frame on the aforementioned robot). Forward kinematics of "floating-base" objects
Consider the special case of having a MultibodyPlant with exactly ane body added, and no joints. The kinematic tree is simply the earth frame, the body frame, and they are connected by the "floating base". What does the forrad kinematics function: $$X^B = f_{kin}^B(q),$$ wait like in that case? If $q$ is already representing the floating-base configuration, is $f^B_{kin}$ just the identity function?
This gets into the subtle points of how we represent transforms, and how we represent rotations in particular. There are many possible representations of 3D rotations, they are good for different things, and unfortunately, there is no one representation to rule them all. (This is one of the many reasons why everything is ameliorate in 2D!) Common representations include 3x3 rotation matrices, Euler angles (east.k. Curlicue-Pitch-Yaw), centrality angle, and unit of measurement quaternions. In Drake, we provide all of these representations, and arrive easy to convert back and along betwixt them. In order to make the spatial algebra efficient, we use rotation matrices in our RigidTransform, merely in lodge to have a more meaty representation of configuration we use unit quaternions in our configuration vector, $q$. You can think of unit quaternions as a class of axis angles that have been carefully normalized to exist unit of measurement length and accept magical properties. My favorite careful description of quaternions is probably chapter 1 of
Every bit a result, for this instance, the software implementation of the function $f_{kin}^B$ is precisely the role that converts the position $\times$ unit quaternion representation into the position $\times$ rotation matrix representation.
Differential kinematics (Jacobians)
The forward kinematics machinery gives u.s. the ability to compute the pose of the gripper and the pose of the object, both in the globe frame. But if our goal is to move the gripper to the object, then nosotros should sympathise how changes in the articulation angles relate to changes in the gripper pose. This is traditionally referred to as "differential kinematics".
At kickoff blush, this is straightforward. The change in pose is related to a change in joint positions past the (partial) derivative of the frontwards kinematics: \begin{equation}dX^B = \pd{f_{kin}^B(q)}{q} dq = J^B(q)dq. \label{eq:jacobian}\end{equation} Partial derivatives of a function are referred to as "Jacobians" in many fields; in robotics it's rare to refer to derivatives of the kinematics as anything else.
All of the subtlety, again, comes in because of the multiple representations that we have for 3D rotations (rotation matrix, unit quaternions, ...). While there is no one best representation for 3D rotations, it is possible to have one approved representation for differential rotations. Therefore, without any loss of generality, we can correspond the rate of modify in pose using a vi-component vector for spatial velocity: \brainstorm{equation}{}^AV^B_C = \brainstorm{bmatrix} {}^A\omega^B_C \\ {}^A\text{v}^B_C \end{bmatrix}.\cease{equation} ${}^AV^B_C$ is the spatial velocity of frame $B$ relative to frame $A$ expressed in frame $C$, ${}^A\omega^B_C \in \Re^3$ is the angular velocity (of frame $B$ relative frame $A$ expressed in frame $C$), and ${}^A\text{five}^B_C \in \Re^3$ is the translational velocity (along with the same shorthands as for positions). Translational and rotational velocities are simply vectors, then they tin can be operated on only similar positions:
- Spatial velocities add together (when the frames friction match): \begin{equation} {}^A\text{5}^B_F + {}^B\text{v}^C_F = {}^A\text{five}^C_F, \qquad {}^A\omega^B_F + {}^B\omega^C_F = {}^A\omega^C_F,\cease{equation} and accept the condiment inverse. For the translational velocity, the improver is possibly known from high-school physics; for the angular velocity I consider it quite surprising, and it deserves to exist verified.
- Rotation matrices tin can be used to change betwixt the "expressed-in" frames when those frames are stock-still: \brainstorm{equation} {}^A\text{v}^B_G = {}^GR^F {}^A\text{v}^B_F, \qquad {}^A\omega^B_G = {}^GR^F {}^A\omega^B_F, \qquad \text{when } {}^Thou\dot{R}^F=0.\end{equation}
-
If the relative pose between 2 frames is not fixed, and so nosotros get slightly more complicated formulas involving vector cross products; they are derived from the derivative of the transform equation and the chain rule. (Click the triangle to expand those details, but consider skipping them for now!)
The angular velocity vector is related to the time-derivative of a rotation matrix via the skew-symmetric (every bit verified by differentiating $RR^T=I$) matrix: \begin{equation} \dot{R}R^T = \dot{R}R^{-1} = \brainstorm{bmatrix} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0 \cease{bmatrix}.\end{equation} Multiplying a vector by this matrix can exist written as a vector-cantankerous product: \begin{equation} \dot{R}R^T p = \dot{R}R^{-1} p = \omega \times p.\end{equation} Therefore, differentiating $${}^Gp^A = {}^GX^F {}^Fp^A = {}^Gp^F + {}^GR^F {}^Fp^A,$$ yields \brainstorm{align} {}^G\text{v}^A =& {}^Chiliad\text{five}^F + {}^G\dot{R}^F {}^Fp^A + {}^GR^F {}^F\text{v}^A \nonumber \\ =& {}^Thou\text{v}^F + {}^G\omega^F \times {}^GR^F {}^Fp^A + {}^GR^F {}^F\text{v}^A.\end{marshal}
There is ane more velocity to exist aware of: I'll utilize $v$ to denote the generalized velocity vector of the plant. While a spatial velocity $^AV^B$ is six components, a translational or angular velocity, $^B\text{v}^C$ or $^B\omega^C$, is three components, the generalized velocity vector is whatever size it needs to exist to encode the time derivatives of the configuration variables, $q$. For the iiwa welded to the world frame, that ways it has seven components. I've tried to be conscientious to typeset each of these v's differently throughout the notes. About ever the distinction is as well clear from the context.
Don't presume $\dot{q} \equiv v$
The unit quaternion representation is iv components, but these must form a "unit of measurement vector" of length 1. Rotation matrices are 9 components, but they must form an orthonormal matrix with $\det(R)=1$. Information technology's pretty great that for changes in rotation, we can use an unconstrained three component vector, what we've called the angular velocity vector, $\omega$. And you actually should utilise it; getting rid of that constraint makes both the math and the numerics improve.
But in that location is one small nuisance that this causes. We tend to desire to think of the generalized velocity as the time derivative of the generalized positions. This works when nosotros have merely our iiwa in the model, and it is welded to the world frame. But nosotros cannot presume this in general; not when floating-base rotations are concerned. As evidence, here is a elementary example that loads exactly i rigid body into the MultibodyPlant, and then prints its Context.
The output looks like this:
Context -------- Time: 0 States: 13 continuous states ane 0 0 0 0 0 0 0 0 0 0 0 0 plant.num_positions() = 7 plant.num_velocities() = 6 Y'all tin can see that this system has 13 total country variables. seven of them are positions, $q$; we use unit quaternions in the position vector. But we have but 6 velocities, $v$; we apply athwart velocities in the velocity vector. Clearly, if the length of the vectors don't even match, we do non take $\dot{q} = v$.
It's not really any harder; Drake provides the MultibodyPlant methods MapQDotToVelocity and MapVelocityToQDot to get back and forth betwixt them. Just you take to recall to use them!
Due to the multiple possible representations of 3D rotation, and the potential difference between $\dot{q}$ and $v$, there are actually many different kinematic Jacobians possible. You lot may hear the terms "analytic Jacobian", which refers to the explicit partial derivative of the forward kinematics (every bit written in \eqref{eq:jacobian}), and "geometric Jacobian" which replaces 3D rotations on the left-hand side with spatial velocities. In Drake's MultibodyPlant, we currently offer the geometric Jacobian versions via
-
CalcJacobianAngularVelocity, -
CalcJacobianTranslationalVelocity, and -
CalcJacobianSpatialVelocity,
Kinematic Jacobians for selection and place
Let'due south repeat the setup from in a higher place, merely we'll impress out the Jacobian of the gripper frame, relative to the world frame, expressed in the earth frame.
Differential inverse kinematics
In that location is important structure in Eq \eqref{eq:jacobian}. Make sure y'all didn't miss it. The relationship between joint velocities and end-effector velocities is (configuration-dependent) linear: \begin{equation}5^G = J^Yard(q)5.\stop{equation} Maybe this gives us what we need to produce changes in gripper frame $G$? If I take a desired gripper frame velocity $5^{G_d}$, then how well-nigh commanding a joint velocity $v = \left[J^G(q)\right]^{-1} V^{G_d}$?
The Jacobian pseudo-changed
Whatever time yous write a matrix inverse, information technology's of import to bank check that the matrix is really invertible. Every bit a first sanity cheque: what are the dimensions of $J^K(q)$? We know the spatial velocity has half-dozen components. Our gripper frame is welded straight on the final link of the iiwa, and the iiwa has seven positions, and then nosotros have $J^G(q_{iiwa}) \in \Re^{6x7}.$ The matrix is not foursquare, so does not accept an inverse. But having more degrees of freedom than the desired spatial velocity requires (more columns than rows) is actually the good instance, in the sense that we might have many solutions for $five$ that can achieve a desired spatial velocity. To cull one of them (the minimum-norm solution), we can consider using the Moore-Penrose pseudo-inverse, $J^+$, instead: \brainstorm{equation}v = [J^G(q)]^+Five^{G_d}.\end{equation}
The pseudo-inverse is a beautiful mathematical concept. When the $J$ is square and full-rank, the pseudo-changed returns the truthful inverse of the organisation. When there are many solutions (here many joint velocities that accomplish the same terminate-effector spatial velocity), then information technology returns the minimum-norm solution (the articulation velocities that produce the desired spatial velocity which are closest to cypher in the least-squares sense). When in that location is no exact solution, it returns the joint velocities that produce an spatial velocity which is as close to the desired end-effector velocity as possible, again in the least-squares sense. And then good!
Our commencement end-effector "controller"
Let'southward write a simple controller using the pseudo-inverse of the Jacobian. First, we'll write a new LeafSystem that defines one input port (for the iiwa measured position), and ane output port (for the iiwa joint velocity command). Inside that arrangement, we'll inquire MultibodyPlant for the gripper Jacobian, and compute the joint velocities that will implement a desired gripper spatial velocity.
To keep things simple for this beginning instance, we'll merely control a constant gripper spatial velocity, and only run the simulation for a few seconds.
Annotation that nosotros exercise have to add one additional arrangement into the diagram. The output of our controller is a desired joint velocity, but the input that the iiwa controller is expecting is a desired articulation position. So we will insert an integrator in between.
I don't expect you to understand every line in this example, but it'due south worth finding the important lines and making sure you tin can change them and encounter what happens!
Congratulations! Things are actually moving now.
Invertibility of the Jacobian
There is a simple check to sympathize when the pseudo-inverse tin can requite an exact solution for any spatial velocity (achieving exactly the desired spatial velocity): the Jacobian must be full row-rank. In this instance, nosotros need $\rank(J) = 6$. But assigning an integer rank to a matrix doesn't tell the unabridged story; for a real robot with (noisy) floating-betoken joint positions, as the matrix gets close to losing rank, the (pseudo-)inverse starts to "blow-up". A better metric, so, is to lookout the smallest singular value; as this approaches goose egg, the norm of the pseudo-inverse volition approach infinity.
Invertibility of the gripper Jacobian
Y'all might have noticed that I printed out the smallest singular value of $J^1000$ in one of the previous examples. Take it for another spin. See if you tin discover configurations where the smallest singular value gets close to zero.
Here's a hint: endeavor some configurations where the arm is very straight, (e.m. driving joint 2 and 4 close to zero).
Another good fashion to find the singularities are to use your pseudo-changed controller to send gripper spatial velocity commands that drive the gripper to the limits of the robot's workspace. Endeavor it and run into! In fact, this is the mutual case, and 1 that we will work hard to avert.
Configurations $q$ for which $\rank(J(q_{iiwa})) < 6$ for a frame of involvement (like our gripper frame $G$) are called kinematic singularities. Effort to avoid going near them if you lot can! The iiwa has many virtues, merely absolutely its kinematic workspace is not one of them. Trust me, if you try to go a big Kuka to reach into a trivial kitchen sink all twenty-four hour period, every day, then you will spend a non-trivial corporeality of time thinking about fugitive singularities.
In exercise, things can become a lot meliorate if we stop bolting our robot base to a fixed location in the world. Mobile bases add complexity, just they are wonderful for improving the kinematic workspace of a robot.
Are kinematic singularities existent?
A natural question when discussing singularities is whether they are somehow real, or whether they are somehow an artifact of the assay. Maybe it is useful to look at an extremely simple case.
Imagine a 2-link arm, where each link has length ane. Then the kinematics reduce to $$p^G = \brainstorm{bmatrix} c_0 + c_{0+1} \\ s_0 + s_{0 + ane} \stop{bmatrix},$$ where I've used the (very mutual) shorthard $s_0$ for $\sin(q_0)$ and $s_{0+ane}$ for $\sin(q_0+q_1)$, etc. The translational Jacobian is $$J^G(q) = \begin{bmatrix} -s_0 - s_{0+1} & -s_{0 + one} \\ c_0 + c_{0 + 1} & c_{0 + 1} \end{bmatrix},$$ and as expected, it loses rank when the arm is at total extension (east.one thousand. when $q_0 = q_1 = 0$ which implies the first row is zippo).
Click here for the animation.
Let'southward move the robot along the $ten$-axis, by taking $q_0(t) = 1-t,$ and $q_1(t) = -two + 2t$. This clearly visits the singularity $q_0 = q_1 = 0$ at time i, and then leaves once more without trouble. In fact, it does all this with a constant articulation velocity ($\dot{q}_0=-i, \dot{q}_1=2$)! The resulting trajectory is $$p^G(t) = \begin{bmatrix} 2\cos(1-t) \\ 0 \finish{bmatrix}.$$
There are a few things to understand. At the singularity, at that place is zip that the robot can do to move its gripper further in positive $x$ -- that singularity is real. But it is likewise true that there is no way for the robot to move instantaneously back in the management of $-x.$ The Jacobian analysis is not an approximation, information technology is a perfect clarification of the human relationship between articulation velocities and gripper velocities. However, simply because you lot cannot attain an instantaneous velocity in the backwards direction, it does not mean you cannot get in that location! At $t=i$, even though the articulation velocities are abiding, and the translational Jacobian is singular, the robot is accelerating in $-ten$, $\ddot{p}^G_{W_x}(t) = -2\cos(i-t).$
Defining the grasp and pre-grasp poses
I'1000 going to put my red foam brick on the table. Its geometry is defined as a vii.5cm 10 5cm x 5cm box. For reference, the distance between the fingers on our gripper in the default "open" position is 10.7cm. The "palm" of the gripper is three.625cm from the body origin, and the fingers are viii.2cm long.
To make things easy to outset, I'll promise to set up the object downwardly on the table with the object frame's $z$-axis pointing upwards (aligned with the world $z$ axis), and you can assume information technology is resting on the table safely within the workspace of the robot. But I reserve the correct to requite the object arbitrary initial yaw. Don't worry, you might have noticed that the seventh joint of the iiwa volition permit you rotate your gripper around quite nicely (well across what my human wrist tin can practise).
Observe that visually the box has rotational symmetry -- I could ever rotate the box 90 degrees around its $ten$-axis and you wouldn't be able to tell the divergence. We'll think about the consequences of that more than in the next affiliate when we first using perception. But for now, nosotros are ok using the omniscient "cheat port" from the simulator which gives us the unambiguous pose of the brick.
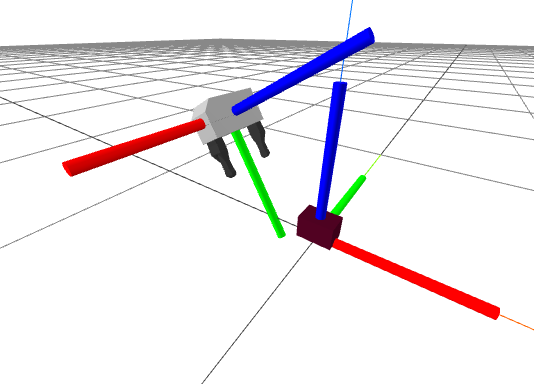
Take a careful expect at the gripper frame in the figure above, using the colors to sympathize the axes. Here is my thinking: Given the size of the hand and the object, I want the desired position (in meters) of the object in the gripper frame, $${}^{G_{grasp}}p^O = \brainstorm{bmatrix} 0 \\ 0.12 \\ 0 \end{bmatrix}, \qquad {}^{G_{pregrasp}}p^O = \begin{bmatrix} 0 \\ 0.2 \\ 0 \cease{bmatrix}.$$ Remember that the logic behind a pregrasp pose is to first movement to safely above the object, if our only gripper motion that is very shut to the object is a straight translation from the pregrasp pose to the grasp pose and back, so information technology allows usa to mostly avoid having to think about collisions (for now). I want the orientation of my gripper to be set so that the positive $z$ centrality of the object aligns with the negative $y$ axis of the gripper frame, and the positive $ten$ axis of the object aligns with the positive $z$ centrality of the gripper. We can accomplish that with $${}^{G_{grasp}}R^O = \text{MakeXRotation}\left(\frac{\pi}{2}\correct) \text{MakeZRotation} \left(\frac{\pi}{2}\correct).$$ I acknowledge I had my right paw in the air for that one! Our pregrasp pose volition accept the same orientation every bit our grasp pose.
Computing grasp and pregrasp poses
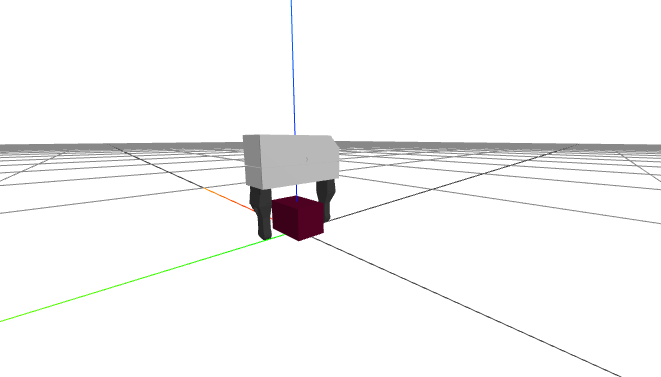
Here is a simple example of loading a floating Schunk gripper and a brick, computing the grasp / pregrasp pose (drawing out each transformation clearly), and rendering the manus relative to the object.
I hope you lot can see the value of having good notation at work here. My right hand was in the air when I was deciding what a suitable relative pose for the object in the hand should be (when writing the notes). Just once that was decided, I went to type it in and everything just worked.
A pick and place trajectory
We're getting close. We know how to produce desired gripper poses, and we know how to alter the gripper pose instantaneously using spatial velocity commands. At present we demand to specify how nosotros want the gripper poses to modify over time, so that we can convert our gripper poses into spatial velocity commands.
Let'south define all of the "keyframe" poses that we'd similar the gripper to travel through, and time that it should visit each one. The post-obit case does precisely that.
A plan "sketch"
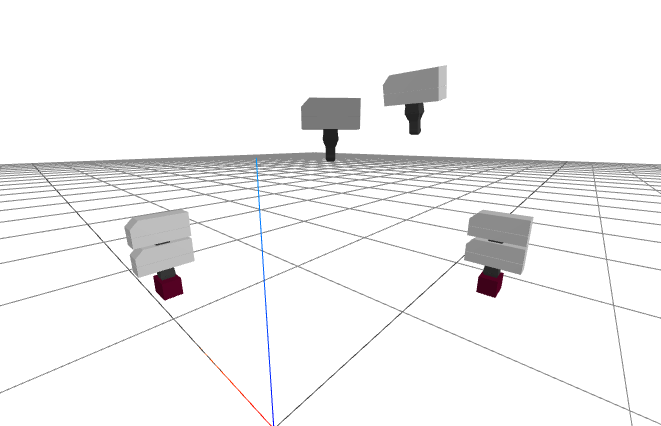
How did I choose the times? I started everything at time, $t=0$, and listed the residue of our times as absolute (time from zero). That's when the robot wakes upward and sees the brick. How long should nosotros take to transition from the starting pose to the pregrasp pose? A really skillful respond might depend on the exact articulation speed limits of the robot, but nosotros're not trying to movement fast yet. Instead I chose a conservative time that is proportional to the total Euclidean altitude that the manus will travel, say $k=x~due south/m$ (aka $10~cm/southward$): $$t_{pregrasp} = k \left\|{}^{G_0}p^{G_{pregrasp}}\right\|_2.$$ I but chose a fixed duration of two seconds for the transitions from pregrasp to grasp and dorsum, and as well left 2 seconds with the gripper stationary for the segments where the fingers needs to open/close.
There are a number of ways one might represent a trajectory computationally. We take a pretty skillful drove of trajectory classes available in Drake. Many of them are implemented as splines -- piecewise polynomial functions of time. Interpolating between orientations requires some intendance, but for positions we tin do a simple linear interpolation between each of our keyframes. That would be called a "first-lodge concord", and it's implemented in Drake's PiecewisePolynomial class. For rotations, we'll apply something called "spherical linear interpolation" or slerp, which is implemented in Drake's PiecewiseQuaternionSlerp, and which you tin can explore in this do. The PiecewisePose course makes it user-friendly to construct and work with the position and orientation trajectories together.
Grasping with trajectories
At that place are a number of means to visualize the trajectory when it's connected to 3D. I've plotted the position trajectory as a function of time below.
For a super interesting discussion on how we might visualize the 4D quaternions as creatures trapped in 3D, y'all might relish this serial of "explorable" videos.
One final detail -- we also need a trajectory of gripper commands (to open and close the gripper). We'll use a first-club hold for that, every bit well.
Putting it all together
Nosotros can slightly generalize our PseudoInverseController to take additional input ports for the desired gripper spatial velocity, ${}^WV^G$ (in our outset version, this was only hard-coded in the controller).
The trajectory we have constructed is a pose trajectory, but our controller needs spatial velocity commands. Fortunately, the trajectory classes we accept used support differentiating the trajectories. In fact, the PiecewiseQuaternionSlerp is clever enough to return the derivative of the 4-component quaternion trajectory as a 3-component athwart velocity trajectory, and taking the derivative of a PiecewisePose trajectory returns a spatial velocity trajectory. The rest is simply a thing of wiring upward the system diagram.
The full pick and place demo
The next few cells of the notebook should get you a pretty satisfying result. Click here to picket it without doing the work.
It's worth scrutinizing the effect. For instance, if you examine the context at the final time, how close did it come to the desired final gripper position? Are you happy with the joint positions? If you ran that same trajectory in reverse, then dorsum and along (equally an industrial robot might), would you expect errors to accumulate?
Differential inverse kinematics with constraints
Our solution above works in many cases. We could potentially move on. Simply with just a little more work, we can go a much more than robust solution... ane that we will exist happy with for many chapters to come.
And then what'south incorrect with the pseudo-inverse controller? You won't exist surprised when I say that information technology does non perform well around singularities. When the minimum singular value of the Jacobian gets small-scale, that means that some values in the changed get very big. If y'all enquire our controller to rails a seemingly reasonable finish-effector spatial velocity, and then you might have extremely big velocity commands that issue.
There are other important limitations, though, which are maybe more subtle. The existent robot has constraints, very real constraints on the articulation angles, velocities, accelerations, and torques. If you, for instance, send a velocity command to the iiwa controller that cannot be followed, that velocity will exist clipped. In the mode we are running the iiwa (joint-impedance mode), the iiwa doesn't know anything well-nigh your end-effector goals. So it will very likely simply saturate your velocity commands independently articulation by joint. The upshot, I'm agape, will not be equally convenient equally a slower stop-effector trajectory. Your end-effector could run wildly off form.
Since nosotros know the limits of the iiwa, a better approach is to accept these constraints into business relationship at the level of our controller. Information technology'south relatively directly-forward to have position, velocity, and dispatch constraints into business relationship; torques would require a full dynamics model so we won't worry nigh them yet here.
Pseudo-changed every bit an optimization
I introduced the pseudo-inverse as having about magical properties: it returns an exact solution when one is available, or the best possible solution (in the least-squares norm) when one is not. These properties can all be understood by realizing that the pseudo-inverse is just the optimal solution to a least-squares optimization problem: \begin{equation} \min_v \left|J^Grand(q)v - 5^{G_d}\right|^2_2. \end{equation} When I write an optimization of this course, I volition refer to $v$ as the conclusion variable(s), and I will use $five^*$ to denote the optimal solution (the value of the determination variables that minimizes the cost). Here we have $$five^* = \left[ J^Thou(q) \correct]^+Five^{G_d}.$$
Optimization is an incredibly rich topic, and we will put many tools from optimization theory to utilise over the course of this text. For a beautiful rigorous but accessible treatment of convex optimization, I highly recommend
Adding velocity constraints
In one case nosotros sympathize our existing solution through the lens of optimization, nosotros have a natural road to generalizing our arroyo to explicitly reason about the constraints. The velocity constraints are the near straight-forward to add. \begin{align} \min_v && \left|J^Chiliad(q)5 - V^{G_d}\right|^2_2, \\ \subjto && v_{min} \le v \le v_{max}. \nonumber \terminate{marshal} Yous tin read this as "find me the joint velocities that attain my desired gripper spatial velocity as closely every bit possible, but satisfy my articulation velocity constraints." The solution to this tin can be much improve than what you would become from solving the unconstrained optimization and then only trimming any velocities to respect the constraints after the fact.
This is, admittedly, a harder trouble to solve in general. The solution cannot be described using merely the pseudo-changed of the Jacobian. Rather, we are going to solve this (small) optimization problem directly in our controller every time it is evaluated. This problem has a convex quadratic objective and linear constraints, so it falls into the class of convex Quadratic Programming (QP). This is a particularly squeamish class of optimization issues where nosotros have very strong numerical tools.
Jacobian-based control with velocity constraints
Adding position and acceleration constraints
We can hands add together more constraints to our QP, without significantly increasing the complication, as long as they are linear in the decision variables. So how should we add together constraints on the joint position and acceleration?
The natural arroyo is to make a first-order approximation of these constraints. To exercise that, the controller needs some feature time stride / timescale to relate its velocity decisions to positions and accelerations. We'll denote that fourth dimension step as $h$.
The controller already accepts the current measured articulation positions $q$ as an input; let the states now also take the current measured articulation velocities $v$ as a second input. And we'll apply $v_n$ for our decision variable -- the adjacent velocity to control. Using a unproblematic Euler approximation of position and starting time-order derivative for dispatch gives u.s.a. the following optimization problem: \begin{align} \min_{v_n} \quad & \left|J^Chiliad(q)v_n - Five^{G_d}\correct|^2_2, \\ \subjto \quad & v_{min} \le v_n \le v_{max}, \nonumber \\ & q_{min} \le q + h v_n \le q_{max}, \nonumber \\ & \dot{v}_{min} \le \frac{v_n - v}{h} \le \dot{v}_{max}. \nonumber \end{marshal}
Joint centering
Our Jacobian is $half dozen \times 7$, and so we really have more degrees of freedom than end-effector goals. This is not simply an opportunity, but a responsibleness. When the column rank of $J^One thousand$ exceeds the row rank, then nosotros have specified an optimization problem that has an infinite number of solutions; and we've left it upwardly to the solver to cull 1. Typically a convex optimization solver does choose something reasonable, similar taking the "analytic center" of the constraints, or a minimum-norm solution for an unconstrained trouble. But why leave this to chance? It's much better for u.s. to completely specify the problem so that there is a unique global optima.
In the rich history of Jacobian-based control for robotics, there is a very elegant thought of implementing a "secondary" control, guaranteed (in some cases) non to interfere with our primary end-effector spatial velocity controller, by projecting it into the nullspace of $J^K$. So in lodge to fully specify the trouble, we will provide a secondary controller that attempts to control all of the joints. Nosotros'll practice that here with a simple articulation-space controller $v = K(q_0 - q)$; this is a proportional controller that drives the robot to its nominal configuration.
Denote $P(q)$ as an orthonormal ground for the kernel of a Jacobian $J$. Traditionally in robotics we implemented this using the pseudo-inverse: $P = (I - J^+J)$, just many linear algebra packages at present provide methods to obtain one more directly. Calculation $Pv \approx Pk(q_0 - q)$ as a secondary objective can exist accomplished with \brainstorm{align}\min_{v_n} \quad & \left|J^G(q)v_n - V^{G_d}\right|^2_2 + \epsilon \left|P(q)\left(v_n - 1000(q_0 - q)\right)\right|^2_2, \\ \subjto \quad & \text{constraints}.\nonumber\end{align} Note the scalar $\epsilon$ that we've placed in front of the secondary objective. In that location is something of import to understand here. If we exercise not take any constraints, and then nosotros tin can remove $\epsilon$ completely -- the secondary chore volition in no way interfere with the chief task of tracking the spatial velocity. However, if there are constraints, and then these constraints can crusade the two objectives to clash (Exercise). So we choice $\epsilon \ll 1$ to give the primary objective relatively more weight. But don't make it as well minor, because that might make the numerics bad for your solver. I'd say $\epsilon ~= 0.01$ is simply about right.
There are more sophisticated methods if ane wishes to constitute a strict task prioritization in the presence of constraints (e.g.
Alternative formulations
Once nosotros have embraced the thought of solving a small optimization problem in our control loop, many other formulations are possible, too. Y'all volition find many in the literature. Minimizing the least-squares altitude between the commanded spatial velocity and the resulting velocity might non actually be the best solution. The formulation we have been using heavily in Drake adds an additional constraint that our solution must motion in the same management every bit the commanded spatial velocity. If nosotros are up against constraints, then we may slow down, just we will not deviate (instantaneously) from the commanded path. It would be a compassion to spend a long time carefully planning collision-gratis paths for your end-effector, just to accept your controller treat the path as but a suggestion. Note, however, that your plan playback organisation however needs to be smart enough to realize that the slow-down occurred (open up-loop velocity commands are not enough).
\brainstorm{align} \max_{v_n, \alpha} \quad & \alpha, \\ \subjto \quad & J^G(q)v_n = \alpha V^{G_d}, \nonumber \\ & 0 \le \blastoff \le 1, \nonumber \\ & \text{boosted constraints}. \nonumber \end{marshal} You should immediately inquire yourself: is it reasonable to scale a spatial velocity by a scalar? That's some other great exercise.
What happens in this conception when the Jacobian drops row rank? Notice that $v_n = 0, \alpha = 0$ is always a feasible solution for this problem. Then if it'south not possible to move in the commanded direction, then the robot volition but finish.
Drake's DifferentialInverseKinematics
We volition utilise this implementation of differential changed kinematics whenever we need to control the cease-effector in the side by side few capacity.
Exercises
Spatial frames and positions.
I've rendered the gripper and the brick with their corresponding body frames. Given the configuration displayed in the figure, which is a possible value for ${^Gp^O}$?
- [0.2, 0, -.two]
- [0, 0.3, .1]
- [0, -.iii, .1]
Which is a possible value for ${^Gp^O_W}$?
The condiment holding of angular velocity vectors.
TODO(russt): Fill this in.
Spherical linear interpolation (slerp)
For positions, we can linearly interpolate between points, i.e. a "first-order hold". When dealing with rotations, nosotros cannot simply linearly interpolate and must instead employ spherical linear interpolation (slerp). The goal of this trouble is to dig into the details of slerp.
To do and then nosotros volition consider the simpler case where our rotations are in $\Re^{ii}$ and can exist represented with complex numbers. Here are the rules of the game: a 2d vector (x,y) will be represented as a circuitous number $z = ten + yi$. To rotate this vector by $\theta$, we volition multiply by $e^{i\theta} = \cos(\theta) + i\sin(\theta).$
- Let's verify that this works. Accept the 2D vector $(10,y) = (one,ane)$. If you convert this vector into a complex number, multiply by $z = eastward^{i\pi/4}$ using circuitous multiplication, and convert the result back to a 2d vector, do you get the expected result? Testify your work and explain why this is the expected result.
Take a infinitesimal to convince yourself that this recipe (going from a 2D vector to a circuitous number, multiply by $eastward^{i\theta}$, and converting back to a 2nd vector) is mathematically equivalent to multiplying the original number by the 2D rotation matrix: $$R(\theta) = \brainstorm{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix}.$$
A frame $F$ has an orientation. We can represent that orientation using the rotation from the world frame, due east.g. $^WR^F$. We've just verified that you tin represent that rotation using a complex number, $e^{i\theta}$. Now assume we want to interpolate between ii orientations, represented by frames $F$ and $Yard$. How should nosotros smoothly interpolate between the two frames, eastward.yard. using $t\in [0,1]$? You'll explore this in parts (b) and (c).
- Attempt one: Consider $z(t) = (a_F*(1-t) + a_G*t) + i (b_F*(one-t) + b_G*t)$. Have $t=.5$. What happens if you multiply the 2D vector $(i,one)$ past $z(t = .5)$? Show your work and explicate what goes wrong.
- Try 2: Instead nosotros can leverage the other representation: $z(t) = eastward^{i \theta_{F}*(1-t) + i\theta_{G}*t}$. What happens if we multiply by the second vector $(ane,ane)$ by $z(t = .five)$? Again, show your piece of work.
Quaternions just are a generalization of this idea to 3D. In second, it might seem inefficient to use two numbers and a constraint that $a^2 + b^ii = 1$ to represent a single rotation (why non only $\theta$!?), simply we've seen that it works. In 3D we can use iv numbers $x,y,z,w$ plus the constraint that $10^2+y^2+z^2+w^2 = one$ to represent a 3D rotation. In 2d, using just $\theta$ tin work fine, merely in 3D using only iii numbers leads to problems like the famous gimbal lock. The 4 numbers forming a unit quaternion provides a non-degenerate mapping of all 3D rotations.
Just like nosotros saw in 2D, i cannot simply linearly interpolate the 4 numbers of the quaternion to interpolate orientations. Instead, we linearly interpolate the angle between two orientations, using the quaternion slerp. The details involve some quaternion notation, only the concept is the same as in 2nd.
Scaling spatial velocity
TODO(russt): Fill this in. Until then, hither'due south a little code that might convince you it's reasonable.
Planar Manipulator
For this do yous will derive the translational forward kinematics ${^A}p{^C}=f(q)$ and the translational Jacobian $J(q)$ of a planar two-link manipulator. You will work exclusively in this notebook. Y'all will exist asked to complete the post-obit steps:
- Derive the forward kinematics of the manipulator.
- Derive the Jacobian matrix of the manipulator.
- Analyze the kinematic singularities of the manipulator from the Jacobian.
Exploring the Jacobian
Exercise three.5 asked you to derived the translational Jacobian for the planar two-link manipulator. In this trouble we volition explore the translational Jacobian in more than detail, both in the context of a planar 2-link manipulator and in the context of a planar three-link manipulator. For the planar three-link manipulator, the joint angles are $(q_{0}, q_{1}, q_{2})$ and the planar terminate-effector position is described by $(x, y)$.
- For the planar two-link manipulator, the size of the planar translational Jacobian is 2x2. What is the size of the planar translational Jacobian of the planar three-link manipulator?
- In considering the planar two-link and three-link manipulators, how does the size of the translational Jacobian impact the type of inverse that can be computed? (when can the changed be computed exactly? when can information technology not?)
- Beneath, for the planar two-link manipulator, we draw the unit circle of joint velocities in the $\dot{\theta_{1}}-\dot{\theta_{two}}$ aeroplane. This circumvolve is then mapped through the translational Jacobian to an ellipse in the end effector velocity space. In other words, this visualizes that the translational Jacobian maps the space of joint velocities to the infinite of terminate-effector velocities.
The ellipse in the stop-effector velocity infinite is called the manipulability ellipsoid. The manipulability ellipsoid graphically captures the robot's ability to move its finish effector in each management. For case, the closer the ellipsoid is to a circle, the more easily the cease effector tin move in arbitrary directions. When the robot is at a singularity, it cannot generate finish effector velocities in certain directions. Thinking back to the singularities you explored in Practice three.5, at i of these singularities, what shape would the manipulability ellipsoid collapse to?
Spatial Transforms and Grasp Pose
For this exercise you will apply your cognition on spatial algebra to write poses of frames in different reference frames, and design a grasp pose yourself. You lot will work exclusively in this notebook. You will exist asked to complete the following steps:
- Express poses of frames in unlike reference frames using spatial algebra.
- Design grasp poses given the configuration of the target object and griper configuration.
The Robot Painter
For this practice yous volition design interesting trajectories for the robot to follow, and detect the robot virtually painting in the air! You lot will piece of work exclusively in this notebook. You will exist asked to consummate the following steps:
- Design and compute the poses of cardinal frames of a designated trajectory.
- Construct trajectories by interpolating through the key frames.
Introduction to QPs
For this exercise you will practice the syntax of solving Quadratic Programs (QPs) via Drake's MathematicalProgram interface. You will work exclusively in this notebook.
Virtual Wall
For this exercise you will implement a virtual wall for a robot manipulator, using an optimization-based approach to differential inverse kinematics. Y'all will work exclusively in this notebook. Y'all will exist asked to consummate the following steps:
- Implement a optimization-based differential IK controller with joint velocity limits.
- Using your own constraints, implement a virtual wall in the end-effector infinite using optimization-based differential IK controller.
Competing objectives
In the department on joint centering, I claimed that an secondary objective might compete with a primary objective if they are linked through constraints. To see this, consider the following optimization problem \begin{marshal*}\min_{ten,y} \quad (x-v)^2 + (y+3)^2.\end{align*} Clearly, the optimal solution is given by $ten^*=5, y^*=-3$. Moreover, the objective are separable. The addition of the 2d objective, $(y+3)^2$, did not in any style impact the solution of the first.
Now consider the constrained optimization \begin{align*}\min_{x,y} \quad& (x-5)^ii + (y+iii)^2 \\ \subjto \quad& x - y \le 6. \finish{align*} If the second objective was removed, then we would all the same take $ten^*=v$. What is the upshot of the optimization as written (information technology'southward only a few lines of lawmaking, if you lot desire to do it that way)? I call back you'll observe that these "orthogonal" objectives actually compete!
What happens if you alter the problem to \begin{align*}\min_{x,y} \quad& (x-5)^two + \frac{ane}{100}(y+iii)^ii \\ \subjto \quad& x - y \le 6? \end{align*} I call back you'll observe that solution is quite close to $x^*=five$, but too that $y^*$ is quite different than that $y^*=0$ 1 would obtain if the "secondary" objective was omitted completely.
Note that if the constraint was not active at the optimal solution (east.g. $ten=5, y=-iii$ satisfied the constraints), then the objectives practise not compete.
This seems like an overly simple case. But I call up you lot'll find that it is actually quite like to what is happening in the nullspace objective conception above.
References
- , "Introduction to Robotics: Mechanics and Control", Pearson Education, Inc , 2005.
- , "A Mathematical Introduction to Robotic Manipulation", CRC Press, Inc. , 1994.
- , "Mod Robotics", Cambridge Academy Press , 2017.
- , "Naive {L}ie theory", Springer Science \& Business concern Media , 2008.
- , "Convex Optimization", Cambridge University Press , 2004.
- , "Command of redundant robots under difficult joint constraints: Saturation in the null infinite", IEEE Transactions on Robotics, vol. 31, no. iii, pp. 637--654, 2015.
- , "Hierarchical quadratic programming: Fast online humanoid-robot motion generation", The International Periodical of Robotics Research, vol. 33, no. 7, pp. 1006--1028, 2014.
Source: http://manipulation.csail.mit.edu/pick.html
0 Response to "Can a 3 Axis Arm Draw a Circle"
ارسال یک نظر